FFTs on the Manifold

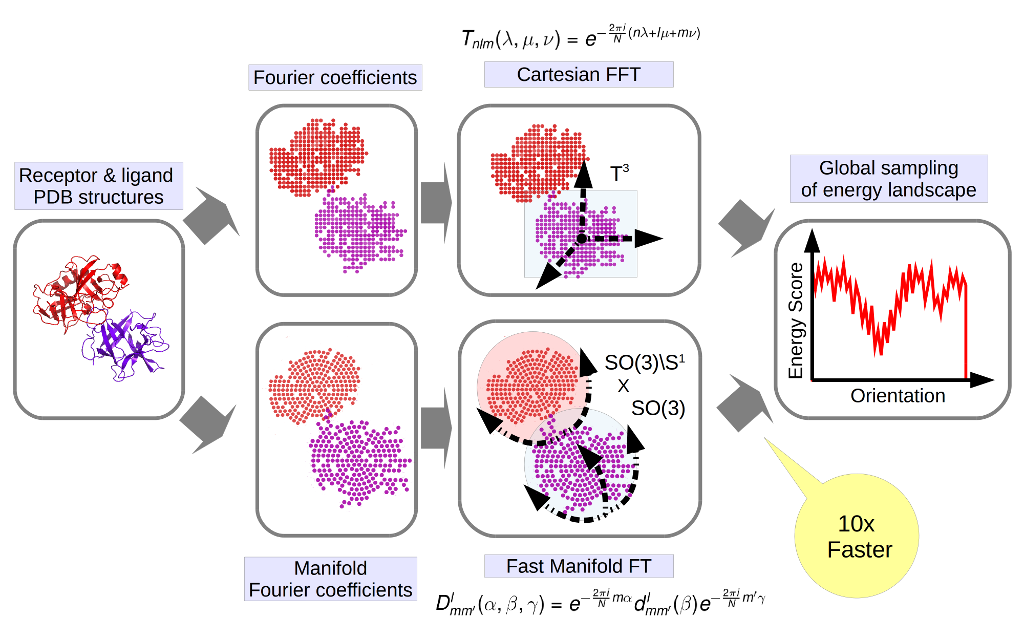
method_compressed_scaled — Figure 1 Comparison of Cartesian and Manifold Fast Fourier transform-based sampling approaches.

The interaction energy between two almost rigid macromolecules can be described as the sum of correlations of characteristic functions defined on the component molecules, which lead to the development of fast Fourier transform (FFT) based docking methods. Considering the receptor protein fixed, traditional FFT methods make an exhaustive scan of the rotations of the ligand, and for each rotation apply the convolution theorem and fast Fourier transforms to rapidly compute correlation functions for all translations. Although the approach deals with just half of the degrees of freedom, the use of FFT still provides substantial numerical advantage. However, this advantage starts to erode, when we want to introduce more complex energy function and, when adding experimental constraints, since each such constraint adds a new correlation function. Instead of using classical decomposition of the encounter complex space to $R(3) \times SO(3)$ we propose to use natural manifold structure of interaction encounter complexes is $SO(3) \times SO(3) \setminus S \times R^1$ manifold. Such decomposition will require only expression of one dimensional translation in rotational coordinates, which is much simpler. We are developing generalization of FFT based approach to such space (manifold FFT) , which searches through 5D manifold space and samples only one translational parameter conventionally, thereby substantially accelerating the search. The greatest advantage of the proposed algorithm is that we calculate the Fourier transforms for the P components of the scoring function only once, perform manifold search in 5 dimension, and for each one-dimensional translation calculate a single inverse Manifold Fourier Transform. Hence using the method can be efficiently used with scoring functions of high complexity, which wasn’t previously possible .

The source code is available at: https://bitbucket.org/abc-group/fmft_suite

[1].

[1]

Padhorny, D., Kazennov, A., Zerbe, B. S., Porter, K. A., Xia, B., Mottarella, S. E., Kholodov, Y., Ritchie, D. W., Vajda, S. & Kozakov, D. (2016) Protein–protein docking by fast generalized fourier transforms on 5d rotational manifolds. IN Proceedings of the national academy of sciences, 113.E4286-E4293.
[Bibtex]

@article{Padhorny26072016,
author = {Padhorny, Dzmitry and Kazennov, Andrey and Zerbe, Brandon S. and Porter, Kathryn A. and Xia, Bing and Mottarella, Scott E. and Kholodov, Yaroslav and Ritchie, David W. and Vajda, Sandor and Kozakov, Dima},
title = {Protein–protein docking by fast generalized Fourier transforms on 5D rotational manifolds},
volume = {113},
number = {30},
pages = {E4286-E4293},
year = {2016},
doi = {10.1073/pnas.1603929113},
abstract ={Energy evaluation using fast Fourier transforms (FFTs) enables sampling billions of putative complex structures and hence revolutionized rigid protein–protein docking. However, in current methods, efficient acceleration is achieved only in either the translational or the rotational subspace. Developing an efficient and accurate docking method that expands FFT-based sampling to five rotational coordinates is an extensively studied but still unsolved problem. The algorithm presented here retains the accuracy of earlier methods but yields at least 10-fold speedup. The improvement is due to two innovations. First, the search space is treated as the product manifold SO(3)×(SO(3)∖S1), where SO(3) is the rotation group representing the space of the rotating ligand, and (SO(3)∖S1) is the space spanned by the two Euler angles that define the orientation of the vector from the center of the fixed receptor toward the center of the ligand. This representation enables the use of efficient FFT methods developed for SO(3). Second, we select the centers of highly populated clusters of docked structures, rather than the lowest energy conformations, as predictions of the complex, and hence there is no need for very high accuracy in energy evaluation. Therefore, it is sufficient to use a limited number of spherical basis functions in the Fourier space, which increases the efficiency of sampling while retaining the accuracy of docking results. A major advantage of the method is that, in contrast to classical approaches, increasing the number of correlation function terms is computationally inexpensive, which enables using complex energy functions for scoring.},
URL = {http://www.pnas.org/content/113/30/E4286.abstract},
eprint = {http://www.pnas.org/content/113/30/E4286.full.pdf},
journal = {Proceedings of the National Academy of Sciences}
}